A captação é o subsistema do SPDA responsável por garantir um local seguro para o acoplamento galvânico do raio. Segundo a NBR 5419-3:2015, é possível projetá-la através do método das malhas, esfera rolante e ângulo de proteção. É importante ressaltar que também é permitido realizar a combinação destes métodos e, desde que atendam aos pré-requisitos listados na tabela 3 da norma, componentes metálicos existentes podem ser aproveitados como captores naturais.
De modo geral, definir qual esquema de captação será utilizado depende bastante das características da estrutura, principalmente, quando existirem elementos acima da superfície de cobertura.
O método da esfera rolante consiste em simular o rolamento de uma esfera com raio pré-definido em função do nível de proteção do SPDA (Tabela 2 da parte 3 da NBR 5914), sobre a edificação. Todo local em que a esfera tocar é considerado um provável ponto de impacto do raio e, consequentemente, é onde deverá ser instalado um captor.
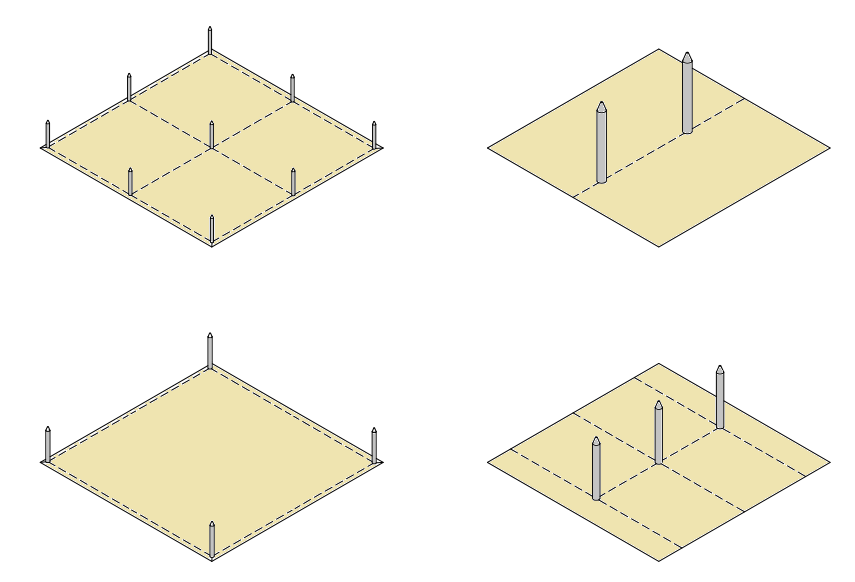
À medida que são adicionados captores, esta simulação deve ser realizada novamente até que a estrutura esteja totalmente protegida, assim como representado na Figura 1. É importante que em edificações com formas geométricas complexas ou com muitos elementos na superfície, o rolamento da esfera seja simulado em vários sentidos, de modo a adequar-se a todas as características existentes.
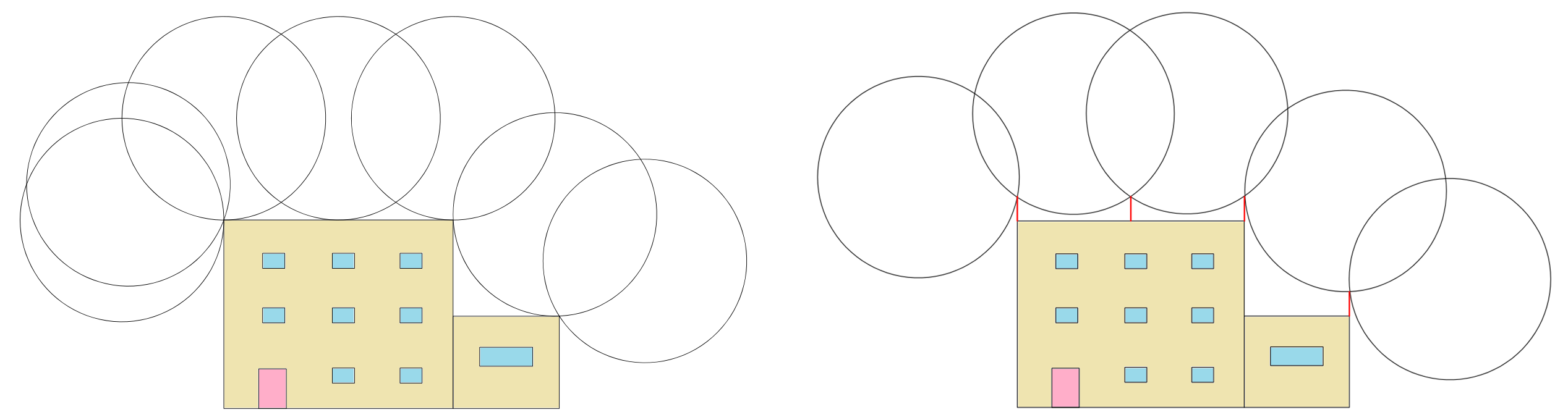

Fonte: Autor/2021.
Por outro lado, quando o telhado é totalmente plano, sem antenas, equipamentos de ar condicionado e outros elementos que alterem a estrutura a ser protegida, o dimensionamento do sistema pode ser simplificado. Basta relacionar a altura dos captores, a distância entre eles e o raio da esfera, assim como representado na Figura 2.
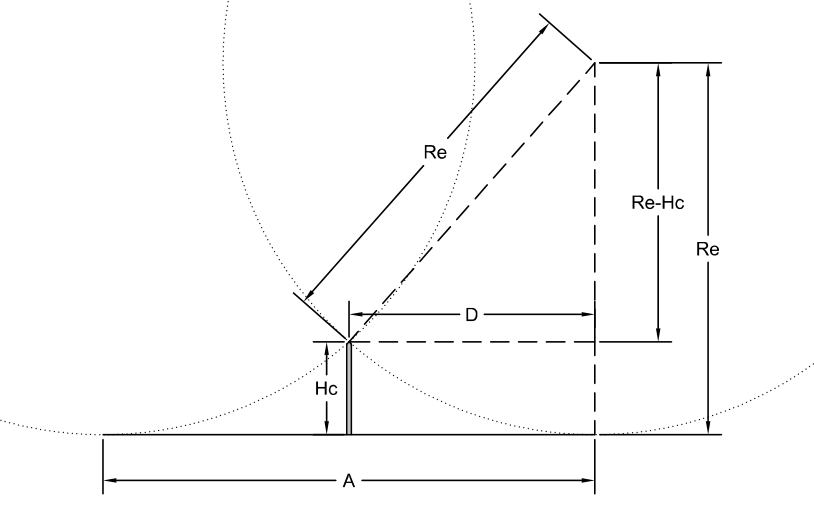

Fonte: Autor/2021.
Para identificar o alcance da proteção oferecido por um captor de altura “Hc” utilizando o método da esfera rolante em um sistema linear, pode-se calcular a distância “D” através da equação abaixo, de acordo com o teorema de Pitágoras.
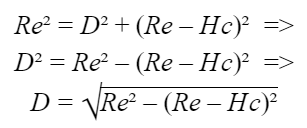
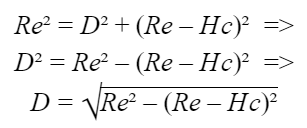
Onde:
Re = raio da esfera rolante (m);
Hc = altura do captor (m);
D = distância linear máxima de proteção a partir do captor (m).
Como os captores oferecem proteção em todos os sentidos, para saber seu alcance linear máximo (em metros) ”A“ basta multiplicar o resultado de “D” por 2.
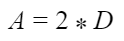
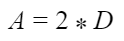
Vale ressaltar que essa equação somente é válida caso exista um condutor de captação em anel circundando os limites da cobertura. Isso porque, ao considerar apenas ”D” como referência para posicionar os captores, a esfera poderá tocar a edificação em suas extremidades, invalidando toda a proteção, assim como representado na Figura 3.
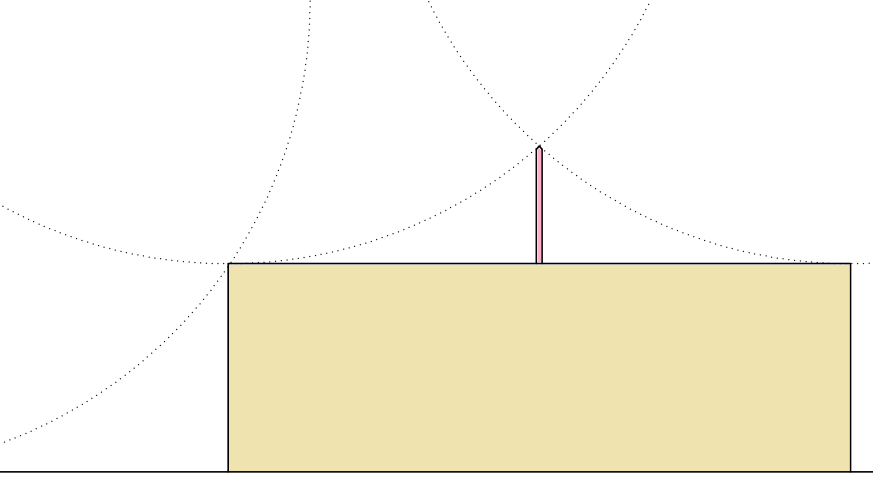

Caso não seja possível circundar a cobertura com um anel de captação, é necessário calcular a distância máxima para afastar os captores da borda da edificação.
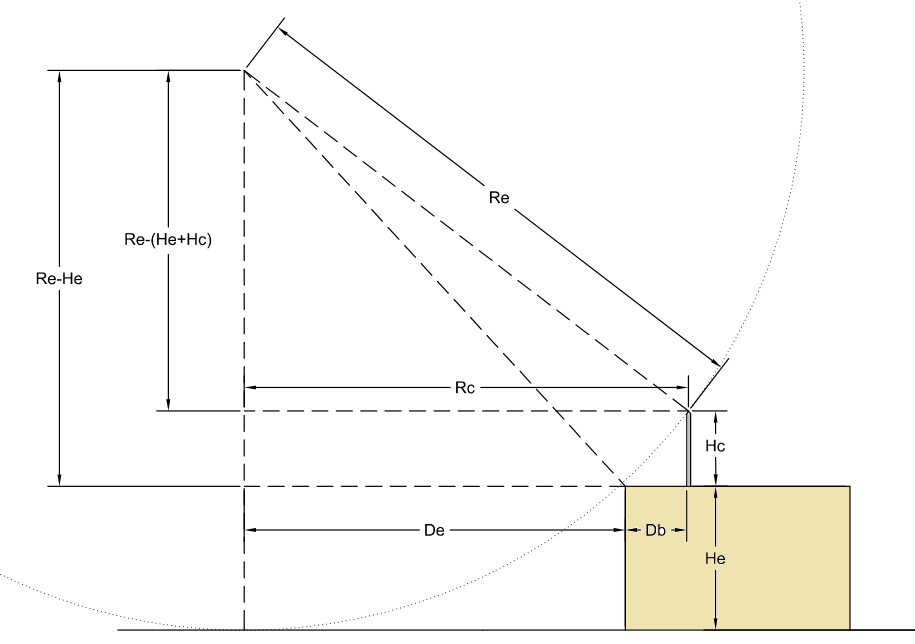

Vamos chamar essa distância entre o captor e a borda de “Db”. Para que Db seja válido é necessário que este satisfaça as seguintes condições:
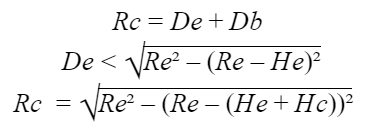
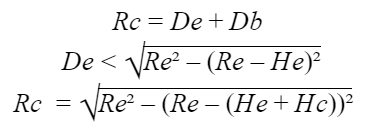
A primeira equação é uma relação matemática simples de comparação, em que o raio de proteção do captor deve ser igual a soma entre a distância externa e a distância da borda ao captor.
A segunda é uma condição a partir do teorema de Pitágoras, que envolve a altura da edificação e o raio da esfera, de modo a evitar que esta toque na edificação.
A terceira condição envolve a altura do captor e o raio da esfera, com o objetivo único de identificar o raio de proteção do captor até o ponto mais afastado da edificação.
Por fim, através da aplicação de sistemas matemáticos entre essas três equações podemos encontrar qual o valor máximo de afastamento Db que o captor poderá ter:
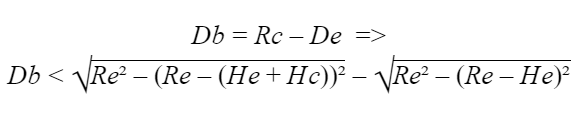
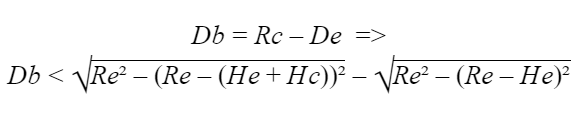
Onde:
Re = raio da esfera rolante (m);
Hc = altura do captor (m);
He = altura da edificação (m);
Rc = raio de proteção do captor (m);
De = distância máxima de proteção contra impactos diretos do raio oferecida por uma edificação (m);
Db = distância do captor até a borda da edificação (m).
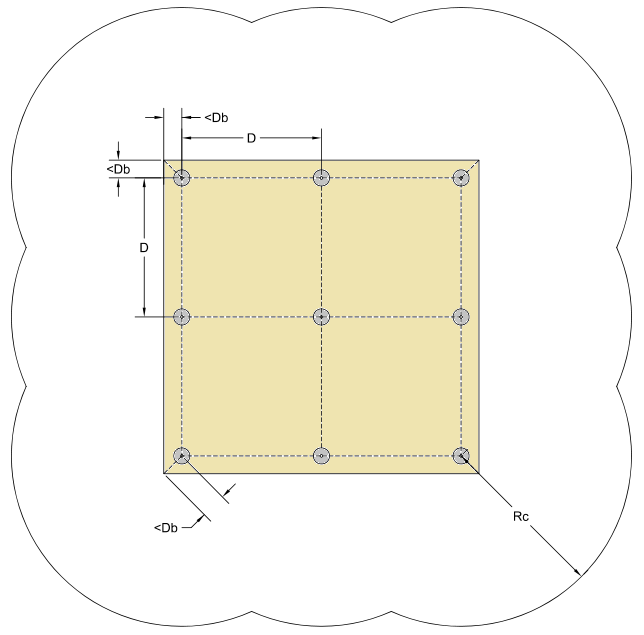

Assim, é possível calcular não somente qual o afastamento máximo entre os captores, como também limitar, em projeto, a distância máxima que estes deverão estar afastados da borda da edificação.
Essas equações são ótimas para agilizar o dimensionamento do método da esfera rolante em superfícies planas, já que podemos colocá-las em uma planilha e, a partir daí, automatizar todo o sistema de captação.
Ainda assim, é preciso ficar atento, pois estes cálculos funcionarão desde que o raio da esfera rolante seja maior que a altura da edificação. Ademais, também devem ser considerados os outros critérios para utilização do método da esfera rolante, tais como: interligar todos os captores e calcular o número de descidas conforme o nível de proteção, sendo o mínimo de 2.

*Nikolas Lemos
Engenheiro de Vendas da Termotécnica Para raios.



Eu já trabalhava deste modo, mais para quem está no início da carreira está bem esclarecedor e tranquilo tecnicamente de se entender
Olá, gostaria de saber qual a altura máxima que as partes energizadas podem ter
Olá, Lucas! Pode entrar em contato com nosso suporte técnico por telefone, por favor?
Assim poderemos entender melhor a situação e discutirmos sobre o assunto.
Nosso telefone é: (31) 3308-7000 ramal 7074 ou 7077.